Phương pháp bình phương bé nhất là kỹ thuật phân tích phức tạp hơn phương pháp cực đại - cực tiểu và có độ chính xác cao hơn. Phương pháp này nhằm xác định phương trình biến thiên của chi phí dựa trên việc tính toán hệ phương trình 2 biến trong phân tích thồng kê, sử dụng số liệu chi phí thực tế phát sinh tương ứng với các mức độ hoạt động của các kỳ đã qua.
Phương trình dự toán chu phí hỗn hợp cũng có dạng tổng quát: Y = a + b.X như phương pháp cực đại - cực tiểu.
Từ phương trình Yi = a + b. Xi, với n lần quan sát, ta có hệ phương trình chuẩn 2 biến sau:
∑XiYi = a.∑Xi + b.∑Xi2 (1)
∑Yi = n.a + b.∑Xi (2)
Trong đó:
Yi: Biến số phụ thuộc - Phản ảnh chi phí hỗn hợp ở mức độ hoạt động Xi
Xi: Biến số độc lập - Phản ánh mức độ hoạt động i
b: Độ dốc đường tuyến tính - Phản ánh hệ số biến phí trên một đơn vị mức độ hoạt động.
a: Hằng số - Phản ánh tổng định phí trong chi phí hỗn hợp
n: Số lần xuất hiện biến số độc lập X
Để giải phương trình chuẩn nhằm xác định các thông số a bà b, ta có thể sử dingj một trong các phương pháp sau:
1. Phương pháp thế (khử biến)
Lấy phương trình (PT) (1) nhân với phần tử trục n của PT (2), ta được PT (3)
∑XiYi .n= n.a.∑Xi + n.b.∑Xi2 (3)
Lấy PT (2) nhân với phần tử trục ∑Xi của PT (1) ta được PT (4)
∑XiYi = n.a ∑Xi+ b.∑Xi2 (2)
Lấy PT (3) - PT (4) ta có phương trình mới chỉ còn biến số b:
∑XiYi = b∑Xi2
=> b = ∑Yi/ ∑Xi
Thay b vào 1 trong 2 phương trình trên ta được trị số của a. Và xây dựng phương trình dự toán chi phí hỗn hợp có dạng Y = a + b.X
Ví dụ:
Một doanh nghiệp muốn xây dựng phương trình dự toán chi phí bảo dưỡng máy mócthiết bị theo yếu tố biến phí và định phí. Dựa vào tài liệu về chi phí bảo dường máy móc thiết bị và số giờ máy hoạt động thực tế được thống kê trong 12 tháng như sau:
|
Tháng (n) |
Sơ giờ máy hoạt động (1.000 giờ) (X) |
Chi phí động lực (1.000đ) (Y) |
X.Y | X2 |
| 1 | 9 |
2.900 |
26.100 | 81 |
| 2 | 7 | 2.400 | 16.800 | 49 |
| 3 | 9 | 2.800 | 25.200 | 81 |
| 4 | 10 | 3.100 | 31.000 | 100 |
| 5 | 12 | 3.500 | 42.000 | 144 |
| 6 | 14 | 3.600 | 50.400 | 196 |
| 7 | 11 | 3.200 | 35.200 | 121 |
| 8 | 12 | 3.300 | 39.600 | 144 |
| 9 | 9 | 3.100 | 27.900 | 81 |
| 10 | 8 | 2.800 | 22.400 | 64 |
| 11 | 7 | 2.200 | 15.400 | 49 |
| 12 | 10 | 2.900 | 29.000 | 100 |
| Σ | 118 | 35.800 | 361.100 | 1.210 |
Sử dụng phương pháp thay thế như sau:
∑XiYi = a.∑Xi + b.∑Xi2 (1)
∑Yi = n.a + b.∑Xi (2)
Thay số liệu vào phương trình (1) và (2):
361.100 = a. 118 + b. 1.210 (1)
35.800= a.12 + b.118 (2)
Giải hệ phương trình ta được a = 1.208,12 và b = 180,53
Phương trình dự toán hàng tháng đối bới chi phí động lực (Y) của doanh nghiệp là:
Y = 1.208,12 + 180,53 . X (ĐV: nghìn đồng)
Trong đó: X là số giờ máy hoạt động tính theo đơn vị 1.000 giờ
Giả sử tháng 1 năm tới, số giờ máy hoạt động dự kiến là 9.500 giờ thì chi phí động lực của tháng này dự tính sẽ là: Y = 1.208,12 + 180,53x 9,5 = 2.923,155 (nghìn đồng)
2. Phương pháp tính theo công thức
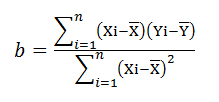hay 
(*)
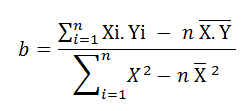Trên thực tế, dựa vào số liệu từ các bảng tính toán từ (*) chia cho n ta có thể áp dụng công thức sau:
(**)
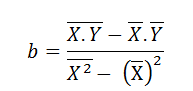Từ số liệu tính toán của phương pháp thế ở trên và áp dụng công thức (**) ta có thể tính b như sau;
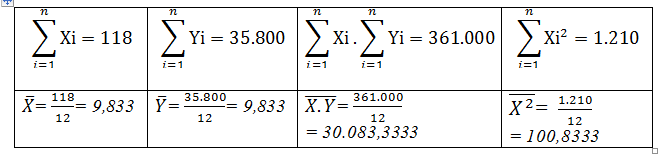
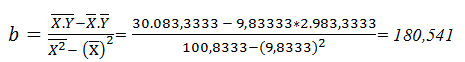
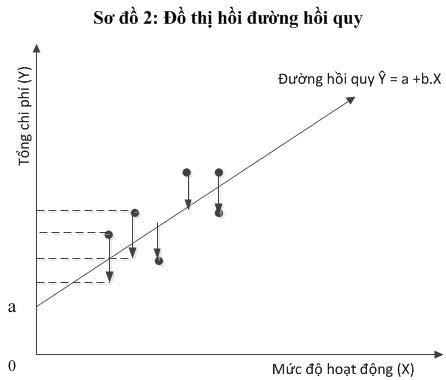
Phương pháp bình phương bé nhất là phương pháp phân tích chi phí hỗn hợp tốt nhất. Bới vì độ chênh lệch giữa đường hồi quy
mà chúng ta thiết lập so với những điểm chi phí hỗn hợp ở từng vị trí 
đạt chênh lệch.
có giá trị tuyệt đối nhỏ nhất. Điều này có nghĩa là khả năng đặc trưng của chi phí hỗm hợp tìm được có độ chính xác cao và mức sai sót (ei) nhỏ nhất. Tuy nhiên, việc tính toán cũng phức tạp hơn phương pháp cực đại - cực tiểu.
Như vậy tôi đã trình bày hết các phương pháo cơ bản thường được sử dụng trong thực tế để xây dựng các phương trình dự toán chi phí hỗn hợp.
Bài sau: "Phân loại chi phí theo mối quan hệ với kỳ tính kết quả kinh doanh"
Phân tích chi phí hỗn hợp (Phương pháp bình phương bé nhất)
bình phương bé nhất Chi phí chi phí hỗn hợp khử biến